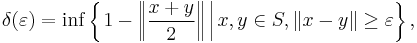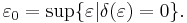Modulus and characteristic of convexity

In mathematics, the modulus and characteristic of convexity are measures of "how convex" the unit ball in a Banach space is. In some sense, the modulus of convexity has the same relationship to the ε-δ definition of uniform convexity as the modulus of continuity does to the ε-δ definition of continuity.

Definitions

The modulus of convexity of a Banach space (X, || ||) is the function δ : [0, 2] → [0, 1] defined by

$\delta (\varepsilon) = \inf \left\{ \left. 1 - \left\| \frac{x %2B y}{2} \right\| \, \right| x, y \in S, \| x - y \| \geq \varepsilon \right\},$

where S denotes the unit sphere of (X, || ||). The characteristic of convexity of the space (X, || ||) is the number ε₀ defined by

$\varepsilon_{0} = \sup \{ \varepsilon | \delta(\varepsilon) = 0 \}.$

These notions are implicit in the general study of uniform convexity by J. A. Clarkson (see below; this is the same paper containing the statements of Clarkson's inequalities). The term "modulus of convexity" appears to be due to M. M. Day (see reference below).

Properties

The modulus of convexity, δ(ε), is a non-decreasing function of ε. (The modulus of convexity need not itself be a convex function of ε.^[1])
(X, || ||) is a uniformly convex space if and only if its characteristic of convexity ε₀ = 0.
(X, || ||) is a strictly convex space (i.e., the boundary of the unit ball B contains no line segments) if and only if δ(2) = 1.

References

^ p. 67 in Lindenstrauss, Joram; Tzafriri, Lior, "Classical Banach spaces. II. Function spaces". Ergebnisse der Mathematik und ihrer Grenzgebiete [Results in Mathematics and Related Areas], 97. Springer-Verlag, Berlin-New York, 1979. x+243 pp.

Beauzamy, Bernard (1985 [1982]). Introduction to Banach Spaces and their Geometry (Second revised ed.). North-Holland. ISBN 0444864164. MR 889253.

Clarkson, James (1936). "Uniformly convex spaces". Trans. Amer. Math. Soc. (American Mathematical Society) 40 (3): 396–414. doi:10.2307/1989630. JSTOR 1989630.

Day, Mahlon (1944). "Uniform convexity in factor and conjugate spaces". Ann. Of Math. (2) (Annals of Mathematics) 45 (2): 375–385. doi:10.2307/1969275. JSTOR 1969275.

Fuster, Enrique Llorens. Some moduli and constants related to metric fixed point theory. Handbook of metric fixed point theory, 133-175, Kluwer Acad. Publ., Dordrecht, 2001. MR 1904276

Lindenstrauss, Joram and Benyamini, Yoav. Geometric nonlinear functional analysis Colloquium publications, 48. American Mathematical Society.

Vitali D. Milman. Geometric theory of Banach spaces II. Geometry of the unit sphere. Uspechi Mat. Nauk, vol. 26, no. 6, 73-149, 1971; Russian Math. Surveys, v. 26 6, 80-159.

Pisier, Gilles (1975). "Martingales with values in uniformly convex spaces". Israel J. Math. 20 (3–4): 326–350. doi:10.1007/BF02760337. MR 394135. http://www.springerlink.com/content/pwh1126545520581/.